ዝርዝር ሁኔታ:
- መግቢያ
- ደረጃ 1 - የፍጥነት መለኪያ
- ደረጃ 2 - ጋይሮስኮፕ
- ደረጃ 3: የፍጥነት መለኪያ እና ጋይሮ ማዋሃድ
- ሁሉንም በአንድ ላይ ማዋሃድ - የፍጥነት መለኪያ እና የጂስትሮስኮፕ መረጃን ማዋሃድ።

ቪዲዮ: የፍጥነት መለኪያ እና ጋይሮ አጋዥ ስልጠና - 3 ደረጃዎች

2024 ደራሲ ደራሲ: John Day | [email protected]. ለመጨረሻ ጊዜ የተሻሻለው: 2024-01-30 07:35

መግቢያ
ይህ መመሪያ በኤሌክትሮኒክስ ፕሮጀክቶቻቸው ውስጥ የፍጥነት መለኪያዎችን እና ጋይሮስኮፖችን እንዲሁም የተቀናጁ የ IMU መሳሪያዎችን (የማይለካ የመለኪያ ክፍል) ለመጠቀም ፍላጎት ላለው ሁሉ የታሰበ ነው።
እኛ እንሸፍናለን-
- የፍጥነት መለኪያ ምን ይለካል?
- ጋይሮስኮፕ (aka ጋሮ) ምን ይለካል?
- ከእነዚህ ዳሳሽ ወደ አካላዊ አሃዶች የሚያገኙትን የአናሎግ-ወደ-ዲጂታል (ADC) ንባብ እንዴት እንደሚቀይሩ (እነዚያ ለአክስሌሮሜትር ፣ ዲግ/ሴ ለ ጋይሮስኮፕ) ይሆናሉ
- ከመሬት አውሮፕላኑ አንጻር ስለ መሣሪያዎ ዝንባሌ ትክክለኛ መረጃ ለማግኘት የፍጥነት መለኪያ እና ጋይሮስኮፕ ንባቦችን እንዴት ማዋሃድ
በጽሁፉ ውስጥ ሁሉ ሂሳቡን በትንሹ ለማቆየት እሞክራለሁ። እርስዎ ሳይን/ኮሲን/ታንጀንት ምን እንደሆኑ ካወቁ እርስዎ በየትኛውም መድረክ ቢጠቀሙም በፕሮጀክትዎ ውስጥ እነዚህን ሀሳቦች መረዳትና መጠቀም መቻል አለብዎት -አርዱዲኖ ፣ ፕሮፔለር ፣ መሰረታዊ ማህተም ፣ የአትሜል ቺፕስ ፣ ማይክሮ ቺፕ ፒሲ ፣ ወዘተ.
የ IMU ክፍልን (ውስብስብ FIR ወይም IIR ማጣሪያዎችን እንደ ካልማን ማጣሪያዎች ፣ ፓርኮች-ማክሌላን ማጣሪያዎች ፣ ወዘተ) ለመጠቀም ውስብስብ ሂሳብ ያስፈልግዎታል ብለው የሚያምኑ ሰዎች አሉ። እነዚያን ሁሉ መመርመር እና አስደናቂ ግን ውስብስብ ውጤቶችን ማግኘት ይችላሉ። ነገሮችን የማብራራት መንገዴ መሠረታዊ ሂሳብ ብቻ ይጠይቃል። በቀላልነት ታላቅ አማኝ ነኝ። ከብዙ የተካተቱ መሣሪያዎች በተጨማሪ የማትሪክስ ስሌቶችን የሚጠይቁ ውስብስብ ስልተ ቀመሮችን ለመተግበር ኃይል እና ሀብቶች የሉትም ቀላል የሆነ ስርዓት ለመቆጣጠር እና ለመከታተል ቀላል ይመስለኛል።
እንደ አዲስ የአይ ኤም አይ ክፍል ፣ Acc_Gyro Accelerometer + Gyro IMU ን እንደ ምሳሌ እጠቀማለሁ። ከዚህ በታች ባሉት ምሳሌዎች ውስጥ የዚህን መሣሪያ መለኪያዎች እንጠቀማለን። ይህ መሣሪያ 2 መሣሪያዎችን ስላካተተ ለመጀመር ጥሩ መሣሪያ ነው።
- LIS331AL (የውሂብ ሉህ) - ባለሶስትዮሽ 2G የፍጥነት መለኪያ - LPR550AL (የውሂብ ሉህ) - ባለ ሁለት ዘንግ ዘንግ እና ጥቅል ፣ 500 ዲግሪ/ሰከንድ ጋይሮስኮፕ
አንድ ላይ የ 5-ዲግሪ የነፃነት የማይለካ የመለኪያ ክፍልን ይወክላሉ። አሁን ያ የሚያምር ስም ነው! የሆነ ሆኖ ፣ ከጌጡ ስም በስተጀርባ በዚህ መመሪያ ውስጥ በዝርዝር የምንሸፍነው እና የምንገልፀው በጣም ጠቃሚ የጥምር መሣሪያ አለ።
ደረጃ 1 - የፍጥነት መለኪያ

ይህንን ክፍል ለመረዳት በአክስሌሮሜትር እንጀምራለን። ስለ አክስሌሮሜትር ሲያስቡ ብዙውን ጊዜ በውስጡ ኳስ ያለው የኩብ ቅርፅ ያለው ሣጥን መቅረጽ ጠቃሚ ነው። እንደ ኩኪ ወይም ዶናት ያለ ሌላ ነገር መገመት ይችላሉ ፣ ግን እኔ ኳስ እገምታለሁ-

ይህንን ሳጥን ምንም የስበት ሜዳዎች በሌሉበት ቦታ ወይም ለዚያ ጉዳይ የኳሱን አቀማመጥ ሊነኩ የሚችሉ ሌሎች መስኮች ከሌሉ - ኳሱ በቀላሉ በሳጥኑ መሃል ላይ ይንሳፈፋል። ሳጥኑ ከማንኛውም የጠፈር አካላት በጣም ርቆ በሚገኝ ውጫዊ ቦታ ውስጥ ነው ፣ ወይም እንደዚህ ያለ ቦታ ቢያንስ ሁሉም ነገር ክብደት በሌለበት በፕላኔቷ ዙሪያ የሚሽከረከርበትን የጠፈር ሥራ ለመገመት አስቸጋሪ ከሆነ መገመት ይችላሉ። ከላይ ካለው ሥዕል ለእያንዳንዱ ዘንግ አንድ ጥንድ ግድግዳ እንደምንመድብ ማየት ይችላሉ (በሳጥኑ ውስጥ ማየት እንድንችል ግድግዳውን Y+ ን አስወግደናል)። እያንዳንዱ ግድግዳ ግፊት ተጋላጭ ነው እንበል። እኛ ሳጥኑን ወደ ግራ በድንገት ብንወስድ (በ 1 ግ = 9.8m/s^2) እናፋጥነዋለን ፣ ኳሱ ግድግዳውን X- ይመታል። ከዚያ ኳሱ በግድግዳው ላይ የሚተገበረውን የግፊት ኃይል እንለካለን እና በኤክስ ዘንግ ላይ የ -1 ግ እሴት እናወጣለን።

እባክዎን የፍጥነት መለኪያው ከተፋጠነ ቬክተር በተቃራኒ አቅጣጫ የሚመራውን ኃይል እንደሚለይ ልብ ይበሉ። ይህ ኃይል ብዙውን ጊዜ የማይንቀሳቀስ ኃይል ወይም ምናባዊ ኃይል ተብሎ ይጠራል። ከዚህ መማር ያለብዎት አንድ ነገር የፍጥነት መለኪያ በአንደኛው ግድግዳ ላይ በተተገበረ ኃይል በኩል በተዘዋዋሪ ፍጥነቱን ይለካል (በእኛ አምሳያ መሠረት በእውነተኛ ህይወት የፍጥነት መለኪያዎች ውስጥ ፀደይ ወይም ሌላ ነገር ሊሆን ይችላል)። ይህ ኃይል በመፋጠን ምክንያት ሊከሰት ይችላል ፣ ግን በሚቀጥለው ምሳሌ እንደምናየው ሁል ጊዜ በመፋጠን ምክንያት አይደለም።
እኛ አምሳያችንን ወስደን በምድር ላይ ብናስቀምጠው ኳሱ በ Z- ግድግዳው ላይ ይወድቃል እና ከታች ባለው ሥዕል ላይ እንደሚታየው በታችኛው ግድግዳ ላይ የ 1 ግ ኃይልን ይተገብራል።

በዚህ ሁኔታ ሳጥኑ አይንቀሳቀስም ነገር ግን አሁንም በ -ዘ ዘንግ ላይ -1 ግ ን እናገኛለን። ኳሱ በግድግዳው ላይ የተጫነበት ግፊት የተፈጠረው በስበት ኃይል ነው። በንድፈ ሀሳብ የተለየ የኃይል ዓይነት ሊሆን ይችላል - ለምሳሌ ፣ ኳሳችን ብረት ነው ብለው ካሰቡ ፣ ማግኔትን ከሳጥኑ አጠገብ ማስቀመጥ ኳሱን ማንቀሳቀስ ስለሚችል ሌላ ግድግዳ እንዲመታ ያደርገዋል። ይህ የተነገረው በመሠረቱ የፍጥነት መለኪያ መለኪያን ኃይልን ማፋጠን አለመሆኑን ለማረጋገጥ ብቻ ነው። ልክ ፍጥነቱ በአክስሌሮሜትር የኃይል ማወቂያ ዘዴ የተያዘ የማይነቃነቅ ኃይል ያስከትላል።
ይህ ሞዴል የ MEMS ዳሳሽ በትክክል እንዴት እንደሚሠራ ባይሆንም ብዙውን ጊዜ የፍጥነት መለኪያ ተዛማጅ ችግሮችን በመፍታት ረገድ ጠቃሚ ነው። በውስጣቸው የብረት ኳሶችን የያዙ ተመሳሳይ ተመሳሳይ ዳሳሾች አሉ ፣ እነሱ የመጠምዘዣ መቀየሪያዎች ተብለው ይጠራሉ ፣ ሆኖም ግን እነሱ በጣም ጥንታዊ ናቸው እና ብዙውን ጊዜ መሣሪያው በተወሰነ ክልል ውስጥ ዝንባሌ ካለው ወይም ካልሆነ ፣ ብቻ የማወቅ ዝንባሌው አይደለም።
እስካሁን ድረስ የፍጥነት መለኪያ ውጤትን በአንድ ዘንግ ላይ ተንትነናል እና ይህ በአንድ ዘንግ አክስሌሮሜትር የሚያገኙት ይህ ብቻ ነው። የ triaxial accelerometers እውነተኛ እሴት የሚመጣው በሦስቱም መጥረቢያዎች ላይ የማይነቃነቁ ኃይሎችን በመለየት ነው። ወደ ሳጥናችን ሞዴል እንመለስ ፣ እና ሳጥኑን 45 ዲግሪ ወደ ቀኝ እናዞረው። ኳሱ አሁን 2 ግድግዳዎችን ይነካል- Z- እና X- ከዚህ በታች ባለው ሥዕል ላይ እንደሚታየው

የ 0.71 እሴቶች የዘፈቀደ አይደሉም ፣ እነሱ በእውነቱ ለ SQRT (1/2) ግምታዊ ናቸው። ቀጣዩን ሞዴላችንን ለአክስሌሮሜትር ስናስተዋውቅ ይህ የበለጠ ግልፅ ይሆናል።
በቀድሞው ሞዴል የስበት ኃይልን አስተካክለን ምናባዊ ሳጥናችንን አዙረናል። ባለፉት 2 ምሳሌዎች ውስጥ ውጤቱን በ 2 የተለያዩ የሳጥን ቦታዎች ላይ ተንትነናል ፣ የኃይል ቬክተር ግን ቋሚ ሆኖ ቆይቷል። ይህ የፍጥነት መለኪያ ከውጭ ኃይሎች ጋር እንዴት እንደሚገናኝ ለመረዳት ጠቃሚ ቢሆንም ፣ አስተባባሪ ስርዓቱን ወደ የፍጥነት መለኪያው ዘንጎች ብናስተካክል እና የኃይል ቬክተር በዙሪያችን እንደሚሽከረከር ብናስብ ስሌቶችን ማከናወን የበለጠ ተግባራዊ ይሆናል።

እባክዎን ከላይ ያለውን ሞዴል ይመልከቱ ፣ ከቀደመው ሞዴል ወደ አዲሱ የአእምሮ ሽግግር ማድረግ እንዲችሉ የመጥረቢያዎቹን ቀለሞች ጠብቄአለሁ። በአዲሱ ሞዴል ውስጥ ያለው እያንዳንዱ ዘንግ በቀድሞው ሞዴል ውስጥ ከሳጥኑ የፊት ገጽታዎች ጋር በቀጥታ የሚገመት መሆኑን ያስቡ። ቬክተር R የፍጥነት መለኪያ የሚለካው የኃይል ቬክተር (ከላይ ከተጠቀሱት ምሳሌዎች የስበት ኃይል ወይም የማይነቃነቅ ኃይል ወይም የሁለቱም ጥምረት ሊሆን ይችላል) ነው። Rx ፣ Ry ፣ Rz በ X ፣ Y ፣ Z axes ላይ የ R ቬክተር ትንበያ ናቸው። እባክዎን የሚከተለውን ግንኙነት ያስተውሉ
R^2 = Rx^2 + Ry^2 + Rz^2 (Eq. 1)
ይህም በ 3 ዲ ውስጥ የፒታጎሪያን ቲዎሪ እኩል ነው።
ያስታውሱ የ SQRT (1/2) ~ 0.71 እሴቶች በዘፈቀደ እንዳልሆኑ ትንሽ ቀደም ብዬ እንደነገርኩዎት ያስታውሱ። ከላይ ባለው ቀመር ውስጥ ከሰኳቸው ፣ የእኛ የስበት ኃይል 1 ግራም መሆኑን ካስታወስን በኋላ ይህንን ማረጋገጥ እንችላለን-
1^2 = (-SQRT (1/2))^2 + 0^2 + (-SQRT (1/2))^2
በቀላሉ R = 1 ፣ Rx = -SQRT (1/2) ፣ Ry = 0 ፣ Rz = -SQRT (1/2) በ Eq.1
ከረዥም የንድፈ ሀሳብ መግቢያ በኋላ ወደ እውነተኛ ሕይወት የፍጥነት መለኪያዎች እየተቃረብን ነው። እሴቶቹ Rx ፣ Ry ፣ Rz በእውነቱ በእውነተኛ የሕይወትዎ የፍጥነት መለኪያ ከሚያመነጩት እና የተለያዩ ስሌቶችን ለማከናወን ሊጠቀሙባቸው ከሚችሏቸው እሴቶች ጋር በቀጥታ ይዛመዳሉ።
እዚያ ከመድረሳችን በፊት የፍጥነት መለኪያዎች ይህንን መረጃ ለእኛ ስለሚያደርሱበት መንገድ ትንሽ እንነጋገር። አብዛኛዎቹ የፍጥነት መለኪያዎች በሁለት ምድቦች ይወድቃሉ -ዲጂታል እና አናሎግ። ዲጂታል የፍጥነት መለኪያዎች እንደ I2C ፣ SPI ወይም USART ያለ ተከታታይ ፕሮቶኮል በመጠቀም መረጃ ይሰጡዎታል ፣ የአናሎግ አክስሌሮተሮች ኤዲሲ (አናሎግ ወደ ዲጂታል መለወጫ) ሞዱል በመጠቀም ወደ ዲጂታል እሴት መለወጥ ያለብዎት አስቀድሞ በተወሰነው ክልል ውስጥ የቮልቴጅ ደረጃን ያወጣሉ። ADC እንዴት እንደሚሠራ ብዙ በዝርዝር አልናገርም ፣ ምክንያቱም በከፊል እንደዚህ ሰፊ ርዕስ ስለሆነ እና በከፊል ከአንድ መድረክ ወደ ሌላ የተለየ ስለሆነ። አንዳንድ ማይክሮ መቆጣጠሪያ የኤዲሲ ልወጣዎችን ለማከናወን አብሮገነብ የኤዲሲ ሞጁሎች ይኖሯቸዋል። ምንም ዓይነት የኤዲሲ ሞዱል ቢጠቀሙ በተወሰነ ክልል ውስጥ እሴት ያገኙታል። ለምሳሌ ባለ 10 -ቢት የኤዲሲ ሞዱል በ 0..1023 ክልል ውስጥ እሴት ያወጣል ፣ ልብ ይበሉ 1023 = 2^10 -1። ባለ 12 ቢት የኤዲሲ ሞዱል በ 0..4095 ክልል ውስጥ እሴት ያወጣል ፣ ልብ ይበሉ 4095 = 2^12-1።
ቀለል ያለ ምሳሌን ከግምት በማስገባት እንቀጥል ፣ የእኛ የ 10 ቢት ኤዲሲ ሞጁል ለሶስቱ የፍጥነት መለኪያ ሰርጦች (መጥረቢያዎች) የሚከተሉትን እሴቶች ሰጥቶናል እንበል -
AdcRx = 586 AdcRy = 630 AdcRz = 561
እያንዳንዱ የኤ.ዲ.ሲ ሞዱል የማጣቀሻ voltage ልቴጅ ይኖረዋል ፣ በእኛ ምሳሌ ውስጥ 3.3 ቪ ነው እንበል። የ 10 ቢት የማስታወቂያ እሴት ወደ ቮልቴጅ ለመለወጥ የሚከተለውን ቀመር እንጠቀማለን
VoltsRx = AdcRx * Vref / 1023
እዚህ ላይ አንድ ፈጣን ማስታወሻ -ለ 8 ቢት አ.ዲ.ሲ የመጨረሻው አከፋፋይ 255 = 2 ^ 8 -1 ፣ እና ለ 12 ቢት ADC የመጨረሻው ከፋይ 4095 = 2 ^ 12 -1 ይሆናል።
ይህንን ቀመር ለሁሉም 3 ሰርጦች ተግባራዊ እናደርጋለን -
VoltsRx = 586 * 3.3V / 1023 = ~ 1.89V (ሁሉንም ውጤቶች ወደ 2 የአስርዮሽ ነጥቦች እናዞራለን) VoltsRy = 630 * 3.3V / 1023 = ~ 2.03V VoltsRz = 561 * 3.3V / 1023 = ~ 1.81V
እያንዳንዱ የፍጥነት መለኪያ ዜሮ-ግ የ voltage ልቴጅ ደረጃ አለው ፣ በዝርዝሮች ውስጥ ሊያገኙት ይችላሉ ፣ ይህ ከ 0 ግ ጋር የሚዛመድ ቮልቴጅ ነው። የተፈረመ የቮልቴጅ እሴት ለማግኘት ከዚህ ደረጃ ያለውን ፈረቃ ማስላት አለብን። የእኛ 0g የቮልቴጅ ደረጃ VzeroG = 1.65V ነው እንበል። እኛ ከዜሮ-ግ ቮልቴጅ የቮልቴጅ ሽግግሮችን እንደሚከተለው እናሰላለን::
ዴልታቮልትስክስ = 1.89 ቪ - 1.65 ቪ = 0.24 ቪ ዴልታቮልትሪ = 2.03 ቪ - 1.65 ቪ = 0.38 ቪ ዴልታ ቮልትዝ = 1.81 ቪ - 1.65 ቪ = 0.16 ቪ
አሁን የእኛ የፍጥነት መለኪያ ንባቦች በቮልት ውስጥ አሉን ፣ አሁንም በ g (9.8 ሜ/ሰ^2) ውስጥ አይደለም ፣ የመጨረሻውን ልወጣ ለማድረግ የፍጥነት መለኪያውን ትብነት ተግባራዊ እናደርጋለን ፣ ብዙውን ጊዜ በ mV/g ውስጥ ይገለጻል። የእኛ ስሜታዊነት = 478.5mV/g = 0.4785V/g እንበል። የስሜታዊነት እሴቶች በአክስሌሮሜትር መለኪያዎች ውስጥ ሊገኙ ይችላሉ። በ g ውስጥ የተገለጹትን የመጨረሻ የኃይል እሴቶችን ለማግኘት የሚከተለውን ቀመር እንጠቀማለን-
Rx = DeltaVoltsRx / ትብነት
Rx = 0.24V / 0.4785V / g = ~ 0.5g Ry = 0.38V / 0.4785V / g = ~ 0.79g Rz = 0.16V / 0.4785V / g = ~ 0.33g
በእርግጥ ሁሉንም ደረጃዎች በአንድ ቀመር ውስጥ ማዋሃድ እንችላለን ፣ ግን እኔ ከኤ ዲሲ ንባቦች በ g ውስጥ ወደተገለጸው የኃይል ቬክተር ክፍል እንዴት እንደሚሄዱ ግልፅ ለማድረግ ሁሉንም ደረጃዎች አልፌያለሁ።
Rx = (AdcRx * Vref / 1023 - VzeroG) / ትብነት (Eq.2) Ry = (AdcRy * Vref / 1023 - VzeroG) / ትብነት Rz = (AdcRz * Vref / 1023 - VzeroG) / ትብነት
እኛ የእኛን የማይንቀሳቀስ ኃይል ቬክተር የሚገልጹ ሁሉም 3 አካላት አሉን ፣ መሣሪያው ከስበት ኃይል ውጭ ለሌላ ኃይሎች የማይገዛ ከሆነ ፣ ይህ የእኛ የስበት ኃይል ቬክተር አቅጣጫ ነው ብለን መገመት እንችላለን። ከመሬት ጋር ሲነፃፀር የመሣሪያውን ዝንባሌ ለማስላት ከፈለጉ በዚህ የቬክተር እና የ Z ዘንግ መካከል ያለውን አንግል ማስላት ይችላሉ። እርስዎም በአንድ ዘንግ የመጠምዘዝ አቅጣጫ ላይ ፍላጎት ካለዎት ይህንን ውጤት በ 2 አካላት መከፋፈል ይችላሉ-በ “X” እና “Y” ዘንግ ላይ በመጠምዘዝ ቬክተር እና በ X / Y መጥረቢያዎች መካከል እንደ ማዕዘን ሊሰላ ይችላል። እነዚህን ማዕዘኖች ማስላት እርስዎ ከሚያስቡት በላይ ቀላል ነው ፣ አሁን እኛ ለ Rx ፣ ለ Ry እና ለ Rz እሴቶችን ስናሰላ። ወደ የመጨረሻው የፍጥነት መለኪያ አምሳያችን እንመለስ እና አንዳንድ ተጨማሪ ማስታወሻዎችን እናድርግ-

እኛ የምንፈልጋቸው ማዕዘኖች በ X ፣ Y ፣ Z axes እና በሀይል ቬክተር አር መካከል ያሉ ማዕዘኖች ናቸው። በ R እና Rx ከተመሰረተው የቀኝ ማዕዘን ሶስት ማዕዘን ማየት ይችላሉ-
cos (Axr) = Rx / R ፣ እና በተመሳሳይ: cos (Ayr) = Ry / R cos (Azr) = Rz / R
ከ Eq.1 ያንን R = SQRT (Rx^2 + Ry^2 + Rz^2) መቀነስ እንችላለን።
የ arccos () ተግባር (የተገላቢጦሽ ኮስ () ተግባር) በመጠቀም የእኛን ማዕዘኖች አሁን ማግኘት እንችላለን-
Axr = arccos (Rx/R) Ayr = arccos (Ry/R) Azr = arccos (Rz/R)
ወደ እነዚህ ቀመሮች ለመምጣት የፍጥነት መለኪያ ሞዴሉን ለማብራራት ረጅም መንገድ ሄደናል። በእርስዎ መተግበሪያዎች ላይ በመመስረት እኛ ያገኘናቸውን ማንኛውንም መካከለኛ ቀመሮችን ለመጠቀም ይፈልጉ ይሆናል። እንዲሁም የጊሮስኮፕ ሞዴልን በቅርቡ እናስተዋውቃለን ፣ እና ይበልጥ ትክክለኛ የዝንባሌ ግምቶችን እንኳን ለማቅረብ የፍጥነት መለኪያ እና የጂስትሮስኮፕ መረጃ እንዴት እንደሚጣመሩ እናያለን።
ግን ያንን ከማድረጋችን በፊት አንዳንድ ተጨማሪ ጠቃሚ ማስታወሻዎችን እናድርግ-
cosX = cos (Axr) = Rx / R ምቹ = cos (Ayr) = Ry / R cosZ = cos (Azr) = Rz / R
ይህ ሶስትዮሽ ብዙውን ጊዜ አቅጣጫ ኮሲን ተብሎ ይጠራል ፣ እና እሱ እንደ አር ቬክተርችን ተመሳሳይ አቅጣጫ ያለው አሃድ ቬክተር (ርዝመት 1 ያለው ቬክተር) ይወክላል። ያንን በቀላሉ ማረጋገጥ ይችላሉ-
SQRT (cosX^2 + ምቹ^2 + cosZ^2) = 1
የ R ቬክተር ሞጁሉን (ርዝመቱን) ከመከታተል ስለሚያድነን ይህ ጥሩ ንብረት ነው። እኛ ብዙውን ጊዜ የእኛን የማይንቀሳቀስ ቬክተር አቅጣጫ የምንፈልግ ከሆነ ሌሎች ስሌቶችን ለማቃለል ሞጁሉን መደበኛ ማድረጉ ምክንያታዊ ነው።
ደረጃ 2 - ጋይሮስኮፕ

እኛ ለአክስሌሮሜትር እንዳደረግነው ለጋይሮስኮፕ ማንኛውንም ተመጣጣኝ የሳጥን ሞዴል አናስተዋውቅም ፣ ይልቁንስ በቀጥታ ወደ ሁለተኛው የፍጥነት መለኪያ ሞዴል እንዘልላለን እና በዚህ ሞዴል መሠረት ጋይሮስኮፕ የሚለካውን እናሳያለን።

እያንዳንዱ ጋይሮስኮፕ ሰርጥ በአንዱ መጥረቢያ ዙሪያ ያለውን ሽክርክሪት ይለካል። ለምሳሌ ባለ 2-መጥረቢያ ጋይሮስኮፕ በዙሪያው ያለውን ሽክርክሪት ይለካዋል (ወይም አንዳንዶች ‹ስለ› ሊሉ ይችላሉ) X እና Y መጥረቢያዎች። ይህንን ሽክርክሪት በቁጥር ለመግለፅ አንዳንድ ማስታወሻዎችን እናድርግ። በመጀመሪያ እንገልፃለን-
Rxz - በ XZ አውሮፕላን Ryz ላይ የማይንቀሳቀስ ኃይል ቬክተር አር ትንበያ ነው - በ YZ አውሮፕላን ላይ የማይንቀሳቀስ ኃይል ቬክተር አር ትንበያ ነው።
በ Rxz እና Rz ከተመሰረተው የቀኝ ማእዘን ሶስት ማእዘን ፣ የፓይታጎሪያን ንድፈ ሃሳብ በመጠቀም እናገኛለን-
Rxz^2 = Rx^2 + Rz^2 ፣ እና በተመሳሳይ - Ryz^2 = Ry^2 + Rz^2
እንዲሁም ልብ ይበሉ
R^2 = Rxz^2 + Ry^2 ፣ ይህ ከ Eq.1 እና ከዚያ በላይ እኩልታዎች ሊገኝ ይችላል ፣ ወይም በ R እና Ryz R^2 = Ryz^2 + Rx^2 ከተሠራው የቀኝ ማዕዘን ሶስት ማዕዘን ሊገኝ ይችላል
እኛ በዚህ ጽሑፍ ውስጥ እነዚህን ቀመሮች አንጠቀምም ነገር ግን በአምሳያችን ውስጥ በሁሉም እሴቶች መካከል ያለውን ግንኙነት ማስተዋል ጠቃሚ ነው።
ይልቁንስ በ Z ዘንግ እና በ Rxz ፣ Ryz vectors መካከል ያለውን አንግል እንደሚከተለው እንገልፃለን-
Axz - በ Rxz (በ XZ አውሮፕላን ላይ የ R ትንበያ) እና የ Z ዘንግ አይዝ መካከል ያለው አንግል - በ Ryz (በ YZ አውሮፕላን ላይ የ R ትንበያ) እና በ Z ዘንግ መካከል ያለው አንግል ነው
አሁን ጋይሮስኮፕ ከሚለካው ጋር እየተቃረብን ነው። ጋይሮስኮፕ ከላይ የተገለጹትን የማዕዘኖች ለውጦች መጠን ይለካል። በሌላ አነጋገር ከነዚህ ማዕዘኖች የለውጥ መጠን ጋር በመስመር የሚዛመድ እሴት ያወጣል። ይህንን ለማብራራት በዘንግ Y ዙሪያ ያለውን የመዞሪያ አንግል (ይህ የአክዝ ማእዘን ይሆናል) በጊዜ t0 እንደለካ እናስብ እና እንደ አክዝ 0 እንገልፃለን ፣ ቀጥሎ ይህንን አንግል በኋለኛው ጊዜ t1 እንለካለን እና እሱ Axz1 ነበር። የለውጡ መጠን እንደሚከተለው ይሰላል።
RateAxz = (Axz1 - Axz0) / (t1 - t0)።
እኛ Axz ን በዲግሪዎች ፣ እና በሰከንዶች ውስጥ የምንገልጽ ከሆነ ፣ ይህ እሴት በ deg/s ውስጥ ይገለጻል። ጋይሮስኮፕ የሚለካው ይህ ነው።
በተግባር ጋይሮስኮፕ (ልዩ ዲጂታል ጋይሮስኮፕ ካልሆነ በስተቀር) በ deg/s ውስጥ የተገለጸውን ዋጋ እምብዛም አይሰጥዎትም። ልክ እንደ የፍጥነት መለኪያ ከኤክ ጋር ተመሳሳይ ቀመር በመጠቀም ወደ deg/s መለወጥ የሚያስፈልግዎትን የኤ.ዲ.ሲ እሴት ያገኛሉ። ለአክስሌሮሜትር የገለፅነው 2። ለጂሮስኮፕ (ዲሲ/ዲ) የመቀየሪያ ቀመር (ኤ.ዲ.ሲ.) እናስተዋውቅ (እኛ የ 10 ቢት ኤዲሲ ሞጁልን እየተጠቀምን ነው ብለን እናስባለን ፣ ለ 8 ቢት ኤዲሲ 1023 ን በ 255 ይተካዋል ፣ ለ 12 ቢት ኤዲሲ 1023 ን በ 4095 ይተካዋል)።
RateAxz = (AdcGyroXZ * Vref / 1023 - VzeroRate) / ትብነት Eq.3 RateAyz = (AdcGyroYZ * Vref / 1023 - VzeroRate) / ትብነት
AdcGyroXZ ፣ AdcGyroYZ - ከእኛ የማስታወቂያ ሞጁል የተገኙ ሲሆን በ YZ አውሮፕላኖች ውስጥ በ RZ ውስጥ የ R ቬክተር ትንበያ ማዞሪያ የሚለካባቸውን ሰርጦች ይወክላሉ።
Vref - ከ VzeroRate በታች ባለው ምሳሌ 3.3V የምንጠቀመው የ ADC ማጣቀሻ ቮልቴጅ ነው - ዜሮ -ደረጃ ቮልቴጅ ነው ፣ በሌላ አነጋገር ፣ ጋይሮስኮፕ ለየትኛውም ሽክርክሪት በማይገዛበት ጊዜ የሚያወጣው ቮልቴጅ ፣ ለ Acc_Gyro ቦርድ እሱ ነው ለምሳሌ 1.23V (ይህንን በመለኪያዎቹ ውስጥ ሊያገኙዋቸው ይችላሉ) ትብነት - የእርስዎ ጋይሮስኮፕ ትብነት በ mV / (deg / s) ውስጥ ብዙውን ጊዜ እንደ mV / deg / s ተብሎ ይፃፋል ፣ እሱ ምን ያህል ኤምቪ እንደሚሆን ይነግርዎታል። የማሽከርከር ፍጥነቱን በአንድ ዲግ/ሰ ከጨመሩ የጂሮስኮስኮፕ ውፅዓት ይጨምራል። የ Acc_Gyro ሰሌዳ ትብነት ለምሳሌ 2mV/deg/s ወይም 0.002V/deg/s ነው
አንድ ምሳሌ እንውሰድ ፣ የእኛ የኤዲሲ ሞዱል የሚከተሉትን እሴቶች ተመለሰ እንበል -
AdcGyroXZ = 571 AdcGyroXZ = 323
ከላይ ያለውን ቀመር በመጠቀም ፣ እና የ Acc_Gyro ሰሌዳ ዝርዝር መግለጫዎችን መለኪያዎች በመጠቀም እናገኛለን-
RateAxz = (571 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ 306 deg/s RateAyz = (323 * 3.3V/1023 - 1.23V)/(0.002V/deg/s) = ~ -94 ዲግሪ/ሰ
በሌላ አነጋገር መሣሪያው በ Y ዘንግ ዙሪያ (ወይም በ XZ አውሮፕላን ውስጥ ይሽከረከራል ማለት) በ 306 ዲግ/ሰ እና በ X ዘንግ (ወይም በ YZ አውሮፕላን ውስጥ ይሽከረከራል ማለት ነው) በ - 94 ዲግ/ሰ. እባክዎን አሉታዊ ምልክት ማለት መሣሪያው ከተለመደው አዎንታዊ አቅጣጫ በተቃራኒ አቅጣጫ ይሽከረከራል ማለት ነው። በስምምነት አንድ የማሽከርከር አቅጣጫ አዎንታዊ ነው። ጥሩ የጊሮስኮፕ ዝርዝር ሉህ የትኛው አቅጣጫ አዎንታዊ እንደሆነ ያሳየዎታል ፣ አለበለዚያ ከመሣሪያው ጋር በመሞከር እና የትኛውን የማዞሪያ አቅጣጫ በውጤቱ ፒን ላይ voltage ልቴጅ እንዲጨምር እንደሚያደርግ በመጥቀስ ማግኘት አለብዎት። ማዞሪያውን እንዳቆሙ ወዲያውኑ ቮልቴጁ ወደ ዜሮ-ደረጃ ደረጃ ስለሚወድቅ ይህ oscilloscope ን በመጠቀም በጣም ጥሩ ነው። መልቲሜትር የሚጠቀሙ ከሆነ ቢያንስ ለጥቂት ሰከንዶች የማያቋርጥ የማዞሪያ መጠንን ጠብቀው በዚህ ሽክርክሪት ወቅት ቮልቴጅን ልብ ይበሉ ፣ ከዚያ ከዜሮ-ደረጃ ቮልቴጅ ጋር ያወዳድሩ። ከዜሮ-ደረጃ ቮልቴጅ የበለጠ ከሆነ የማሽከርከሪያው አቅጣጫ አዎንታዊ ነው ማለት ነው።
ደረጃ 3: የፍጥነት መለኪያ እና ጋይሮ ማዋሃድ

ሁሉንም በአንድ ላይ ማዋሃድ - የፍጥነት መለኪያ እና የጂስትሮስኮፕ መረጃን ማዋሃድ።
ይህን ጽሑፍ እያነበቡ ከሆነ ምናልባት የ IMU መሣሪያን ለማግኘት ወይም ለማቀድ እያቀዱ ከሆነ ፣ ወይም ምናልባት ከተለየ የፍጥነት መለኪያ እና ጋይሮስኮፕ መሣሪያዎች አንዱን ለመገንባት እያሰቡ ይሆናል።
የፍጥነት መለኪያ እና ጋይሮስኮፕን የሚያዋህድ ጥምር የ IMU መሣሪያን ለመጠቀም የመጀመሪያው እርምጃ የእነሱን አስተባባሪ ሥርዓቶች ማስተካከል ነው። ይህንን ለማድረግ ቀላሉ መንገድ የአክስሌሮሜትር አስተባባሪ ስርዓትን እንደ ማጣቀሻ አስተባባሪ ስርዓት መምረጥ ነው። አብዛኛዎቹ የፍጥነት መለኪያ ውሂብ ሉሆች ከአካላዊ ቺፕ ወይም ከመሣሪያው ምስል አንጻር የ X ፣ Y ፣ Z መጥረቢያዎችን አቅጣጫ ያሳያሉ። ለምሳሌ ለ Acc_Gyro ሰሌዳ ዝርዝሮች ውስጥ እንደሚታየው የ X ፣ Y ፣ Z መጥረቢያ አቅጣጫዎች እዚህ አሉ

ቀጣዩ ደረጃዎች የሚከተሉት ናቸው
ከላይ ከተብራሩት ከ RateAxz ፣ RateAyz እሴቶች ጋር የሚዛመዱ የጂስትሮስኮፕ ውጤቶችን ይወቁ። ከአክስሌሮሜትር ጋር በተዛመደ የጂሮስኮፕ አካላዊ አቀማመጥ ምክንያት እነዚህ ውጤቶች ተገላቢጦሽ መሆን እንዳለባቸው ይወስኑ።
አንድ ጋይሮስኮፕ X ወይም Y የሚል ምልክት ካለው ይህ የፍጥነት መለኪያ አስተባባሪ ስርዓት ውስጥ ካለው ማንኛውም ዘንግ ጋር ይዛመዳል ብለው አያስቡ ፣ ምንም እንኳን ይህ ውፅዓት የአይ ኤምዩ ክፍል ቢሆንም። በጣም ጥሩው መንገድ እሱን መሞከር ነው። ከአክስሌሮሜትር ጋር ሲነፃፀር የጂሮስኮስኮፕን አቀማመጥ አስተካክለዋል። የጊሮ እና የፍጥነት መለኪያ ድንበሮች እርስ በእርስ ትይዩ ናቸው ተብሎ ይገመታል ፣ ማለትም ጋይሮውን ከአክስሌሮሜትር ቺፕ አንፃር በ 90 ዲግ ባለ ብዙ ማእዘን ላይ ያስቀምጣሉ። የ IMU ቦርድ ካገኙ አስቀድመው በዚህ መንገድ የተስተካከሉ ሊሆኑ ይችላሉ። ጋይሮስኮፕ ከአክስሌሮሜትር (45 ወይም 30 ዲግሪዎች እንበል) አንጻራዊ በሆነ ማዕዘን ላይ በሚቀመጥበት በዚህ ጽሑፍ ሞዴሎች ውስጥ አንወያይም ፣ ምንም እንኳን ይህ በአንዳንድ መተግበሪያዎች ውስጥ ጠቃሚ ሊሆን ይችላል።
ከዚህ በላይ ከተብራራው የ RateAxz እሴት ጋር የትኛው የ gyroscope ውፅዓት እንደሚወሰን ለመወሰን የናሙና ቅደም ተከተል እዚህ አለ።
- መሣሪያውን በአግድመት አቀማመጥ ከማስቀመጥ ይጀምሩ። ሁለቱም የ X እና Y የፍጥነት መለኪያ ውጤቶች ዜሮ-ግ ቮልቴጅን ያመርታሉ (ለምሳሌ ለ Acc_Gyro ቦርድ ይህ 1.65V ነው)
- ቀጣዩ መሣሪያውን በ Y ዘንግ ዙሪያ ማሽከርከር ይጀምሩ ፣ በሌላ መንገድ መሣሪያውን በ XZ አውሮፕላን ውስጥ ማሽከርከር ነው ፣ ስለሆነም የ X እና Z የፍጥነት መለኪያ ውጤቶች ይለወጡ እና የ Y ውፅዓት ቋሚ ሆኖ ይቆያል። - መሣሪያውን የማያቋርጥ የፍጥነት ማስታወሻ በሚሽከረከርበት ጊዜ የጊሮስኮፕ ውፅዓት በሚቀየርበት ጊዜ ፣ ሌሎች የጊሮስኮፕ ውጤቶች ቋሚ ሆነው መቆየት አለባቸው - በ Y ዘንግ ዙሪያ (በ XZ አውሮፕላን ውስጥ መሽከርከር) በሚሽከረከርበት ጊዜ የተለወጠው የጊሮስኮፕ ውፅዓት ለ AdcGyroXZ የግብዓት ዋጋን ይሰጣል ፣ እኛ RateAxz ን እናሰላለን - የመጨረሻው እርምጃ የማሽከርከሪያው አቅጣጫ ከእኛ ሞዴል ጋር የሚዛመድ መሆኑን ማረጋገጥ ነው ፣ በአንዳንድ አጋጣሚዎች ከአክስሌሮሜትር ጋር በተዛመደ ጋይሮስኮፕ በአካላዊ አቀማመጥ ምክንያት የ RateAxz እሴትን መቀልበስ ሊኖርብዎት ይችላል - መሣሪያውን ዙሪያውን በማዞር ከላይ ያለውን ሙከራ እንደገና ያከናውኑ። የ Y ዘንግ ፣ በዚህ ጊዜ የ X የፍጥነት መለኪያ (AdcRx በእኛ አምሳያ) ይከታተላል። AdcRx የሚያድግ ከሆነ (ከአግድመት አቀማመጥ የመጀመሪያው 90 ዲግሪ ማሽከርከር) ፣ ከዚያ AdcGyroXZ እንዲሁ ማደግ አለበት። ያለበለዚያ RateAxz ን መገልበጥ ያስፈልግዎታል ፣ በ Eq.3 ውስጥ የምልክት ምክንያትን እንደሚከተለው በማስተዋወቅ ይህንን ማሳካት ይችላሉ-
RateAxz = InvertAxz * (AdcGyroXZ * Vref / 1023 - VzeroRate) / ትብነት ፣ InvertAxz 1 ወይም -1 በሆነበት
መሣሪያውን በኤክስ ዘንግ ዙሪያ በማሽከርከር ለ RateAyz ተመሳሳይ የሙከራ ዱላ መደረግ አለበት ፣ እና የትኛውን የጂሮስኮፕ ውጤት ከ RateAyz ጋር እንደሚዛመድ ፣ እና መገልበጥ ካለበት መለየት ይችላሉ። አንዴ ለ InvertAyz ዋጋ ካገኙ ፣ RateAyz ን ለማስላት የሚከተለውን ቀመር መጠቀም አለብዎት ፦
RateAyz = InvertAyz * (AdcGyroYZ * Vref / 1023 - VzeroRate) / ትብነት
እነዚህን ሙከራዎች በ Acc_Gyro ሰሌዳ ላይ ካደረጉ የሚከተሉትን ውጤቶች ያገኛሉ -
- ለ RateAxz የውጤት ፒን GX4 እና InvertAxz = -1 ነው። - ለ RateAyz የውጤት ፒን GY4 እና InvertAyz = -1 ነው
ከዚህ ነጥብ ጀምሮ ለአክስር ፣ ለአይር ፣ ለአዝር (በተገለጸው ክፍል 1. አክስሌሮሜትር) እና ለ RateAxz ፣ RateAyz (በክፍል 2. ጋይሮስኮፕ እንደተገለፀው) ትክክለኛ እሴቶችን ማስላት በሚችሉበት መንገድ የእርስዎን ኢምዩ ማዋቀርዎን እናስባለን።). በመቀጠል ከመሬቱ አውሮፕላን አንፃር የመሣሪያውን ዝንባሌ የበለጠ ትክክለኛ ግምት በማግኘት ጠቃሚ በሚሆኑት በእነዚህ እሴቶች መካከል ያለውን ግንኙነት እንመረምራለን።
በዚህ ነጥብ ላይ እራስዎን እየጠየቁ ሊሆን ይችላል ፣ የፍጥነት መለኪያ አምሳያ ቀድሞውኑ የአክስርን ፣ የአይርን ፣ የአዝርን ዝንባሌ ማዕዘኖችን ከሰጠን ለምን እኛ በጂሮስኮፕ መረጃ ላይ መጨነቅ እንፈልጋለን? መልሱ ቀላል ነው የፍጥነት መለኪያ ውሂብ ሁል ጊዜ 100%ሊታመን አይችልም። በርካታ ምክንያቶች አሉ ፣ የፍጥነት መለኪያ የማይንቀሳቀስ ኃይልን እንደሚለካ ያስታውሱ ፣ እንዲህ ዓይነቱ ኃይል በስበት (እና በጥሩ ሁኔታ በስበት ብቻ) ሊከሰት ይችላል ፣ ነገር ግን በመሣሪያው ፍጥነት (እንቅስቃሴ) ምክንያት ሊሆን ይችላል። በውጤቱም የፍጥነት መለኪያ በአንጻራዊ ሁኔታ በተረጋጋ ሁኔታ ውስጥ ቢሆንም ፣ አሁንም ለንዝረት እና በአጠቃላይ ሜካኒካዊ ጫጫታ በጣም ስሜታዊ ነው። አብዛኛዎቹ የአይኤምአይ ስርዓቶች ማንኛውንም የፍጥነት መለኪያ ስህተቶችን ለማቃለል ጋይሮስኮፕ የሚጠቀሙበት ዋነኛው ምክንያት ይህ ነው። ግን ይህ እንዴት ይደረጋል? እና ጋይሮስኮፕ ከድምፅ ነፃ ነው?
ጋይሮስኮፕ ከጩኸት ነፃ አይደለም ፣ ግን ማሽከርከርን ስለሚለካ ፣ ለሜካኒካዊ እንቅስቃሴዎች አነስተኛ ተጋላጭ ነው ፣ የፍጥነት መለኪያ የሚሠቃየው የጩኸት ዓይነት ፣ ሆኖም ጋይሮስኮፕዎች እንደ የችግር ዓይነቶች (ለምሳሌ ወደ መንሸራተት (ወደ ዜሮ-ተመን እሴት አለመመለስ)) ማሽከርከር ሲቆም)። የሆነ ሆኖ ከአክስሌሮሜትር እና ከግሮሮስኮፕ የሚመጣውን አማካይ መረጃ የፍጥነት መለኪያ ውሂቡን ብቻ በመጠቀም ከምናገኘው በአንፃራዊነት የተሻለ የአሁኑን የመገጣጠሚያ ግምት ማግኘት እንችላለን።
በቀጣዮቹ ደረጃዎች በካልማን ማጣሪያ ውስጥ በተጠቀሙባቸው አንዳንድ ሀሳቦች የተነሳሳውን ስልተ -ቀመር እገልጻለሁ ፣ ሆኖም ግን በተካተቱ መሣሪያዎች ላይ ለመተግበር በጣም ቀላል እና ቀላል ነው። ከዚያ በፊት የእኛ ስልተ ቀመር እንዲሰላ የምንፈልገውን በመጀመሪያ እንይ። ደህና ፣ እኛ ስለ መሣሪያችን ዝንባሌ ሀሳብ የሚሰጠን እንደ Axr ፣ Ayr ፣ Azr ወይም cosX ፣ ምቹ ፣ cosZ ያሉ ሌሎች እሴቶችን የምናገኝበት የስበት ኃይል ቬክተር R = [Rx ፣ Ry ፣ Rz] አቅጣጫ ነው። ከመሬት አውሮፕላኑ አንጻር ፣ በእነዚህ እሴቶች መካከል ያለውን ግንኙነት በክፍል 1. እንወያይበታለን። አንድ ሰው ሊል ይችላል - በክፍል 1 ውስጥ እነዚህ እሴቶች Rx ፣ Ry ፣ Rz ከ Eq.2 የለንምን? ደህና ፣ አዎ ፣ ግን እነዚህ እሴቶች ከአክስሌሮሜትር መረጃ ብቻ የተገኙ መሆናቸውን ያስታውሱ ፣ ስለዚህ በቀጥታ በመተግበሪያዎ ውስጥ ለመጠቀም ከፈለጉ መተግበሪያዎ ከሚታገሰው በላይ ብዙ ጫጫታ ሊያገኙ ይችላሉ። ተጨማሪ ግራ መጋባትን ለማስወገድ የፍጥነት መለኪያዎችን እንደሚከተለው እንገልፃቸው-
Racc - የሚከተሉትን ክፍሎች (በ X ፣ Y ፣ Z axes ላይ ያሉ ትንበያዎች) ያካተተ በአክስሌሮሜትር የሚለካው የማይንቀሳቀስ ኃይል ቬክተር ነው።
RxAcc = (AdcRx * Vref / 1023 - VzeroG) / ትብነት RyAcc = (AdcRy * Vref / 1023 - VzeroG) / ትብነት RzAcc = (AdcRz * Vref / 1023 - VzeroG) / ትብነት
እስካሁን ከአክስሌሮሜትር ኤዲሲ እሴቶች ብቻ ልናገኝ የምንችላቸው የመለኪያ እሴቶች ስብስብ አለን። ይህንን የውሂብ ስብስብ “ቬክተር” ብለን እንጠራዋለን እና የሚከተለውን ማስታወሻ እንጠቀማለን።
Racc = [RxAcc, RyAcc, RzAcc]
እነዚህ የ Racc ክፍሎች ከአክስሌሮሜትር መረጃ ሊገኙ ስለሚችሉ እኛ ወደ ስልተ ቀመርችን ግብዓት ልንወስደው እንችላለን።
እባክዎን ያስተውሉ ምክንያቱም Racc የስበት ኃይልን ስለሚለካ ከዚህ በታች የተገለጸው የቬክተር ርዝመት እኩል ወይም ወደ 1 ግ ቅርብ ነው ብለው ካሰቡ ትክክል ይሆናሉ።
| Racc | = SQRT (RxAcc^2 + RyAcc^2 + RzAcc^2) ፣
ሆኖም ይህንን vector እንደሚከተለው ማዘመን ምክንያታዊ መሆኑን እርግጠኛ ለመሆን-
ዘረኛ (የተለመደ) = [RxAcc/| Racc | ፣ RyAcc/| Racc | ፣ RzAcc/| Racc |]።
ይህ የተለመደው የ Racc vector ርዝመትዎ ሁል ጊዜ 1 መሆኑን ያረጋግጣል።
በመቀጠል አዲስ ቬክተር እናስተዋውቃለን እና እንጠራዋለን
እረፍት = [RxEst, RyEst, RzEst]
ይህ የእኛ ስልተ ቀመር ውጤት ይሆናል ፣ እነዚህ በጂሮስኮፕ መረጃ ላይ በመመርኮዝ እና ባለፈው ግምታዊ መረጃ ላይ በመመርኮዝ የተስተካከሉ እሴቶች ናቸው።
የእኛ ስልተ ቀመር የሚከተለው ነው - - የፍጥነት መለኪያ ይነግረናል - “አሁን እርስዎ በሬክ ቦታ ላይ ነዎት” - እኛ “አመሰግናለሁ ፣ ግን እኔ ልፈትሽ” እንላለን ፣ - ከዚያ ይህንን መረጃ በጂሮስኮስኮፕ ውሂብ እንዲሁም ካለፈው የእረፍት ውሂብ እና አዲስ የተገመተ የቬክተር እረፍት እናወጣለን። - ዕረፍትን እንደ የመሣሪያው ወቅታዊ አቀማመጥ እንደ “ምርጥ ውርርድ” እንቆጥረዋለን።
እንዴት እንዲሠራ ማድረግ እንደምንችል እስቲ እንመልከት።
የፍጥነት መለኪያችንን በማመን እና በመመደብ የእኛን ቅደም ተከተል እንጀምራለን-
እረፍት (0) = ዘር (0)
በነገራችን ላይ እረፍት እና ራክ ቬክተሮች መሆናቸውን ያስታውሱ ፣ ስለዚህ ከላይ ያለው ቀመር 3 የእኩልታ ስብስቦችን ለመፃፍ እና ድግግሞሽን ለማስወገድ ቀላል መንገድ ነው።
RxEst (0) = RxAcc (0) RyEst (0) = RyAcc (0) RzEst (0) = RzAcc (0)
በመቀጠል በ T ሰከንዶች በእኩል የጊዜ ገደቦች መደበኛ ልኬቶችን እናደርጋለን ፣ እና እንደ Racc (1) ፣ Racc (2) ፣ Racc (3) እና የመሳሰሉትን የምንለካቸውን አዲስ መለኪያዎች እናገኛለን። እንዲሁም በእያንዳንዱ ጊዜ እረፍት (1) ፣ እረፍት (2) ፣ ዕረፍት (3) እና የመሳሰሉት አዳዲስ ግምቶችን እናወጣለን።
ደረጃ n ላይ ነን እንበል። ልንጠቀምባቸው የምንፈልጋቸው ሁለት የታወቁ የእሴቶች ስብስቦች አሉን-
እረፍት (n -1) - የቀደመው ግምታችን ፣ በእረፍት (0) = Racc (0) Racc (n) - የአሁኑ የአሁኑ የፍጥነት መለኪያ
ዕረፍትን (n) ከመቁጠርዎ በፊት ፣ እኛ ከግሮስኮፕ እና ከቀድሞው ግምት የምናገኘውን አዲስ የሚለካ እሴት እናስተዋውቅ።
እኛ Rgyro ብለን እንጠራዋለን ፣ እንዲሁም እሱ 3 አካላትን ያካተተ ቬክተር ነው-
Rgyro = [RxGyro ፣ RyGyro ፣ RzGyro]
ይህንን ቬክተር አንድ አካል በአንድ ጊዜ እናሰላለን። በ RxGyro እንጀምራለን።

በ Rz እና Rxz ከተመሰረተው የቀኝ ማዕዘን ሶስት ማእዘን እኛ በእኛ ጋይሮስኮፕ ሞዴል ውስጥ የሚከተለውን ግንኙነት በመመልከት እንጀምር።
tan (Axz) = Rx/Rz => Axz = atan2 (Rx, Rz)
Atan2 ከዚህ በፊት በጭራሽ የማይጠቀሙበት ተግባር ሊሆን ይችላል ፣ በአታን ከተመለሰው (-PI/2 ፣ PI/2) በተቃራኒ (-PI/2 ፣ PI/2) ውስጥ እሴቶችን ካልመለሰ በስተቀር ከአታን ጋር ተመሳሳይ ነው ፣ እና ይወስዳል ከአንድ ይልቅ 2 ክርክሮች። በ 360 ዲግሪ (-PI ወደ PI) ሙሉ ክልል ውስጥ የ Rx ፣ Rz ሁለቱን እሴቶች ወደ ማዕዘኖች እንድንቀይር ያስችለናል። ስለ atan2 እዚህ የበለጠ ማንበብ ይችላሉ።
ስለዚህ RxEst (n-1) ን እና RzEst (n-1) ን ማወቅ እናገኛለን-
Axz (n-1) = atan2 (RxEst (n-1) ፣ RzEst (n-1))።
ያስታውሱ ጋይሮስኮፕ የአክዝ ማእዘኑን የለውጥ መጠን ይለካል። ስለዚህ አዲሱን ማእዘን Axz (n) እንደሚከተለው መገመት እንችላለን-
Axz (n) = Axz (n-1) + RateAxz (n) * ቲ
ያስታውሱ RateAxz ከእኛ ጋይሮስኮፕ ADC ንባቦች ሊገኝ ይችላል። ይበልጥ ትክክለኛ ቀመር እንደሚከተለው የተሰላው አማካይ የማዞሪያ መጠንን መጠቀም ይችላል-
RateAxzAvg = (RateAxz (n) + RateAxz (n-1)) / 2 Axz (n) = Axz (n-1) + RateAxzAvg * T
እኛ ማግኘት የምንችለው በተመሳሳይ መንገድ
Ayz (n) = Ayz (n-1) + RateAyz (n) * ቲ
እሺ አሁን አሁን አክዝ (n) እና አይዝ (n) አሉን። RxGyro/RyGyro ን ለመቀነስ ከዚህ ወዴት እንሄዳለን? ከኤክ. 1 የቬክተር Rgyro ርዝመትን እንደሚከተለው መጻፍ እንችላለን-
| ሪግሮ | = SQRT (RxGyro^2 + RyGyro^2 + RzGyro^2)
እንዲሁም የእኛን የ Racc vector ን መደበኛ ስለሆንን ፣ ርዝመቱ 1 ነው እና ከማሽከርከር በኋላ አልተለወጠም ብለን እንገምታለን ፣ ስለዚህ በአንፃራዊነት ለመፃፍ ደህንነቱ የተጠበቀ ነው-
| ሪግሮ | = 1
ከዚህ በታች ላሉት ስሌቶች ጊዜያዊ አጭር አጻጻፍ እንውሰድ።
x = RxGyro ፣ y = RyGyro ፣ z = RzGyro
ከላይ ያሉትን ግንኙነቶች በመጠቀም የሚከተሉትን መጻፍ እንችላለን-
x = x / 1 = x / SQRT (x^2+y^2+z^2)
የቁጥር እና የቁጥር አመላካች በ SQRT (x^2 + z^2) እንከፋፈል
x = (x / SQRT (x^2 + z^2)) / SQRT ((x^2 + y^2 + z^2) / (x^2 + z^2))
ልብ ይበሉ x / SQRT (x^2 + z^2) = sin (Axz) ፣ ስለዚህ
x = ኃጢአት (Axz) / SQRT (1 + y^2 / (x^2 + z^2))
አሁን በ SQRT ውስጥ ያለውን ክፍልፋይ ቁጥር እና አመላካች በ z^2 ያባዙ
x = ኃጢአት (Axz) / SQRT (1 + y^2 * z^2 / (z^2 * (x^2 + z^2))))
ልብ ይበሉ z / SQRT (x^2 + z^2) = cos (Axz) እና y / z = tan (Ayz) ፣ ስለዚህ በመጨረሻ -
x = ኃጢአት (Axz) / SQRT (1 + cos (Axz)^2 * tan (Ayz)^2)
ወደ ማስታወቃችን ስንመለስ እናገኛለን -
RxGyro = ኃጢአት (Axz (n)) / SQRT (1 + cos (Axz (n))^2 * tan (Ayz (n))^2)
ያንን እናገኛለን በተመሳሳይ መንገድ
RyGyro = ኃጢአት (Ayz (n)) / SQRT (1 + cos (Ayz (n))^2 * tan (Axz (n))^2)
አሁን በመጨረሻ እኛ ማግኘት እንችላለን-
RzGyro = Sign (RzGyro)*SQRT (1 - RxGyro^2 - RyGyro^2)።
RzGyro> = 0 በሚሆንበት ጊዜ ምልክት (RzGyro) = 1 እና RzGyro ሲፈረም (RzGyro) = -1 <R.
ይህንን ለመገመት አንድ ቀላል መንገድ መውሰድ ነው
ምልክት (RzGyro) = ምልክት (RzEst (n-1))
RzEst (n-1) ወደ 0. በሚጠጋበት ጊዜ በተግባር ይጠንቀቁ። በዚህ ጉዳይ ላይ የጂሮውን ደረጃ ሙሉ በሙሉ መዝለል እና መመደብ ይችላሉ- Rgyro = እረፍት (n-1)። አርዝ የአክዝና የአይዝ ማእዘኖችን ለማስላት እንደ ማጣቀሻ ሆኖ ያገለግላል እና ወደ 0 በሚጠጋበት ጊዜ እሴቶች ሊበዙ እና መጥፎ ውጤቶችን ሊያስከትሉ ይችላሉ። ታን () / atan () የተግባር አተገባበር ትክክለኛነት በሌለበት በትላልቅ ተንሳፋፊ ነጥብ ቁጥሮች ጎራ ውስጥ ይሆናሉ።
ስለዚህ እስካሁን ያለንን እንከልሰው ፣ እኛ በእኛ ስልተ ቀመር ደረጃ n ላይ ነን እና የሚከተሉትን እሴቶች አስለናል
እሽቅድምድም - ከአሁኑ የፍጥነት መለኪያ Rgyro - የአሁኑ ንባቦች - ከእረፍት (n -1) እና ከአሁኑ ጋይሮስኮፕ ንባቦች የተገኘ
የዘመነውን ግምት (n) ለማስላት የትኞቹን እሴቶች እንጠቀማለን? ምናልባት ሁለቱንም እንጠቀማለን ብለው ገምተው ይሆናል። እኛ ክብደት ያለው አማካይ እንጠቀማለን ፣ ስለዚህ-
እረፍት (n) = (Racc * w1 + Rgyro * w2) / (w1 + w2)
የክፍልፋዩን ቁጥር እና አመላካች በ w1 በመከፋፈል ይህንን ቀመር ቀለል ማድረግ እንችላለን።
እረፍት (n) = (Racc * w1/w1 + Rgyro * w2/w1)/(w1/w1 + w2/w1)
እና w2/w1 = wGyro ን ከተካ በኋላ እናገኛለን-
እረፍት (n) = (Racc + Rgyro * wGyro) / (1 + wGyro)
ከዚህ በላይ ባለው ፎረምላ wGyro ከእኛ የፍጥነት መለኪያ ጋር ሲነጻጸር የእኛን ጋይሮ ምን ያህል እንደምናምን ይነግረናል። ይህ እሴት በሙከራ ሊመረጥ ይችላል ብዙውን ጊዜ በ 5..20 መካከል ያሉ እሴቶች ጥሩ ውጤቶችን ያስገኛሉ።
ከካልማን ማጣሪያ የዚህ ስልተ -ቀመር ዋና ልዩነት ይህ ክብደት በአንፃራዊነት የተስተካከለ ነው ፣ በካልማን ማጣሪያ ውስጥ የፍጥነት መለኪያ ንባቦች በሚለካው ጫጫታ ላይ በመመርኮዝ ክብደቶቹ በቋሚነት ይዘመናሉ። የካልማን ማጣሪያ “ምርጡን” የንድፈ -ሀሳብ ውጤቶችን ለእርስዎ በመስጠት ላይ ያተኮረ ሲሆን ይህ ስልተ ቀመር ለተግባራዊ ትግበራዎ “በቂ” ውጤቶችን ሊሰጥዎት ይችላል። እርስዎ በሚለኩዋቸው አንዳንድ የጩኸት ሁኔታዎች ላይ በመመስረት wGyro ን የሚያስተካክለውን ስልተ ቀመር መተግበር ይችላሉ ፣ ግን ቋሚ እሴቶች ለአብዛኞቹ ትግበራዎች በደንብ ይሰራሉ።
የዘመኑ ግምታዊ እሴቶቻችንን ለማግኘት አንድ እርምጃ እንቀራለን -
RxEst (n) = (RxAcc + RxGyro * wGyro) / (1 + wGyro) RyEst (n) = (RyAcc + RyGyro * wGyro) / (1 + wGyro) RzEst (n) = (RzAcc + RzGyro * wGyro) / (1 + wGyro)
አሁን ይህንን ቬክተር እንደገና መደበኛ እናድርገው-
R = SQRT (RxEst (n)^2 + RyEst (n)^2 + RzEst (n)^2)
RxEst (n) = RxEst (n)/R RyEst (n) = RyEst (n)/R RzEst (n) = RzEst (n)/R
እና የእኛን ዑደት እንደገና ለመድገም ዝግጁ ነን።
ይህ መመሪያ በመጀመሪያ በ starlino.com ላይ ታየ ፣ ጥቂት ቀላል አርትዖቶችን አድርጌ በፍቃድ እንደገና እለጥፈዋለሁ። አመሰግናለሁ ስታርሊኖ!
የሚመከር:
ADXL345 ን እና ቅንጣት ፎቶን በመጠቀም የፍጥነት መለኪያ - 4 ደረጃዎች

ADXL345 ን እና ቅንጣት ፎቶን በመጠቀም የማፋጠን ልኬት-ADXL345 እስከ ± 16 ግ ድረስ ባለ ከፍተኛ ጥራት (13-ቢት) ልኬት ያለው ትንሽ ፣ ቀጭን ፣ እጅግ በጣም ትንሽ ኃይል ፣ 3-ዘንግ የፍጥነት መለኪያ ነው። የዲጂታል ውፅዓት ውሂብ እንደ 16-ቢት ሁለት ተሞልቶ በ I2 C ዲጂታል በይነገጽ በኩል ተደራሽ ነው። ይለካል
MPU 6050 Gyro ፣ የፍጥነት መለኪያ ከአርዱዲኖ ጋር (Atmega328p): 5 ደረጃዎች
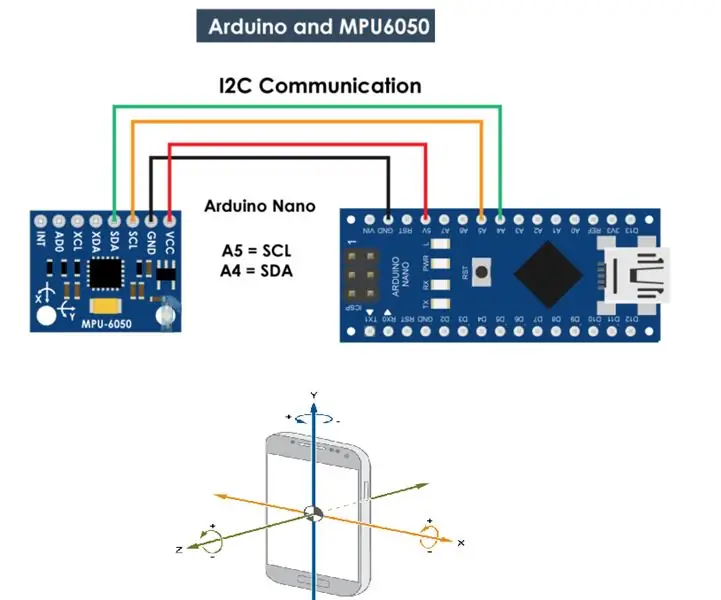
MPU 6050 Gyro ፣ የፍጥነት መለኪያ ከአርዱዲኖ ጋር (Atmega328p): MPU6050 አይኤምዩ በአንድ ቺፕ ላይ የተቀናጀ 3-Axis accelerometer እና 3-Axis gyroscope አለው። X ፣ Y እና Z ዘንግ። የጊሮስኮፕ ውጤቶች አር
የፍጥነት መቆጣጠሪያ እና የርቀት መለኪያ ያለው በብሉቱዝ ቁጥጥር የሚደረግበት RC መኪና 8 ደረጃዎች

የፍጥነት መቆጣጠሪያ እና የርቀት ልኬት ያለው ብሉቱዝ የሚቆጣጠረው አርሲ መኪና - በልጅነቴ ሁል ጊዜ በ RC መኪናዎች ይማርከኝ ነበር። በአሁኑ ጊዜ በአርዱዲኖ እገዛ ርካሽ ብሉቱዝ የሚቆጣጠሩ የ RC መኪናዎችን እራስዎ ለማድረግ ብዙ ትምህርቶችን ማግኘት ይችላሉ። አንድ እርምጃ ወደፊት እንውሰድ እና ተግባራዊ የሆነውን የኪነቲክስ እውቀታችንን ለመቁጠር እንጠቀም
የፍጥነት መለኪያ ጃኬት 5 ደረጃዎች
የአክስሌሮሜትር ጃኬት - ለ ‹KOllision runway› ትርኢት ከዲዛይነር ሚኒካ ኮ ጋር ለመተባበር በ ThunderLily የተነደፈ ፣ አሴለር · ኦምኤተር ጃኬት ፋሽንን ፣ ቴክኖሎጂን እና ሥነ ጥበብን ያጣምራል። የእንቅስቃሴውን አቅጣጫ ለመለየት የፍጥነት መለኪያ በመጠቀም ፣ የእፅዋት ማይክሮፕሮሰሰር
የበይነመረብ የፍጥነት መለኪያ 9 ደረጃዎች (ከስዕሎች ጋር)

የበይነመረብ የፍጥነት መለኪያ - በሕንድ ውስጥ ሙሉ በሙሉ መቆለፊያ በመካሄድ ላይ ፣ የደብዳቤ አገልግሎቶችን ጨምሮ ሁሉም ነገር ተዘግቷል። ምንም አዲስ የፒ.ሲ.ቢ. ፕሮጀክቶች የሉም ፣ አዲስ ክፍሎች የሉም ፣ ምንም የለም! ስለዚህ መሰላቸትን ለማሸነፍ እና እራሴን በሥራ ላይ ለማዋል ፣ ከምቀበላቸው ክፍሎች አንድ ነገር ለማድረግ ወሰንኩ
